Sometime back I took the Coursera online course “Model Thinking” offered by Professor Scott Page.
It covered modeling to help make sense of our complex world. Since models are often simplifications about what really happens, having multiple models that you can apply means you are better able to make sense of the world. I would highly recommend taking the class if you want to be a better citizen and a better thinker.
At one point the class covered very familiar ground. John Conway’s Game of Life and Stephen Wolfram’s cellular automota studies made an appearance, which got me much more enthusiastic about learning how to combine simple methods for complex procedural generation. Along the way came Markov Processes.
Wikipedia says, “A Markov process is a stochastic model that has the Markov property.” Let’s break that down into something resembling everyday language.
Stochastic essentially means random. We’re dealing with a probability. So a Markov process is a model that involves a random element.
And the Markov property? All this part says is that in order to determine what state you are going to be in, the only thing that matters is what state you are currently in. How you got to your current state, otherwise known as your history, is irrelevant. Your past does not determine your future except to the extent that it somehow got you to your present circumstances.
So the simpler definition of a Markov process is that it is a state machine in which how you get to the next state is randomly determined with probabilities based on your current state.
Why is this idea valuable to know?
Let’s say you have weather play a role in your strategy game. If it is raining, your players can’t launch aircraft.
The thing about real weather is that it’s hard to predict. Weather reports tell you that it will be partly cloudy with a 15% chance of rain instead of saying that it will definitely not rain. Because sometimes even if they think it isn’t likely, it happens. Sometimes when they think there will be 4 inches of snow, we find that it is more like half an inch and the predicted snowpocalypse will hit some other city instead. People can talk about the weather as if it is completely random and wonder why meteorologists can keep their jobs when they are wrong so often.
If you wanted to model weather in your game, you could probably use a random number generator. Let’s say that for each day represented in the game, you create a weather report by getting a random number to represent the chance of rain:
1 | int chanceOfRain = rand() % 100; |
So when it comes to determining if it actually should be raining or not, you can create a random number and see if it falls within the value:
1 2 3 4 | bool didItRainToday(){ return (rand() % 100) < chanceOfRain;} |
It would work well enough. Players can make plans based on the forecast, but there are problems.
First, you can’t prevent streaks of certain values from appearing. If you have aircraft in the game, but the weather system prevents you from using them, they become less useful. One day of bad weather might be a minor setback for your war plans, but having weeks of bad weather could be seen by the player as ridiculous. With random number generators, it’s possible to get into this situation, and your players can get frustrated with the bad luck.
Second, you can’t prevent initial values from being “bad” either. The beginning of the game is when you are trying to pull new players into your game’s world. If the game immediately starts with bad luck, it might leave a bad taste in the player’s mouth.
Third, it’s not as realistic to have a day of sunny weather followed by a day of stormy weather followed by a day of sunny weather. As unpredictable as the weather can be, and as possible as the wild swings are, people expect good weather to follow good weather, and bad weather to follow bad weather, and that we’ll have good weather days more often than bad weather days.
You can mitigate the above issues by hardcoding non-rain values for the first few days and also keeping a count of bad weather and forcing good weather if that count goes above a certain threshold, but it’s a clunky solution that still leaves a lot out of your control as a game designer.
Enter Markov chains
Instead of treating each day as completely independent of the next, you can keep track of your current day’s weather state.
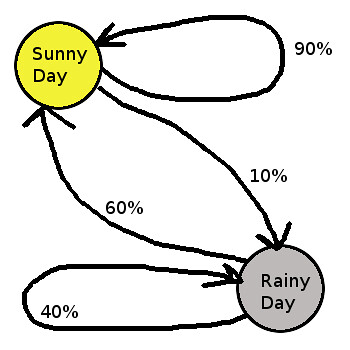
Let’s say that a non-rainy day today has a 90% chance of producing another non-rainy day tomorrow, and that a rainy day has a 60% chance of a sunny day following it.
So almost all of the time a sunny day predicts a sunny day to follow, but every so often it will predict a rainy day. Rainy days might stay rainy for days at a time, but most of the time it will become sunny again the next day. So players can get a feel for how likely rain is to occur and make decisions based on their own mental model of the system, which makes rain an ever present threat without making it an overwhelming or unfair one.
And as a game designer, you can tweak the probabilities of each state until the weather acts how you want it to without having to hardcode everything, create a hacky bandage for it, or give up control to a random number generator completely. You could add more states, such as partly cloudy days and overcast days, which will have different probabilities for moving to other states. Overcast days can result in rainy days more often than sunny days, just like in real life.
You could also put Markov chains to work for you in other areas of games. What if the population of your city simulation has mood swings? That is, if people are content, they are likely to stay content, but sometimes a situation occurs in which enough people get upset that they influence other people to become upset as well. That is, you could have a Markov chain in which content people are likely to be content but sometimes become discontent, and if they are discontent, they are likely to stay discontent but sometimes become content again, mimicking what happens in real life when there is outrage that dies down after the news cycle stops covering the political scandal. In the city simulation, it might drive the player to take actions to address the population’s concerns before real damage occurs.
Or you could create random terrain with roads. Roads tend to want to go straight, but sometimes they turn 90 degrees. Your terrain generator can start creating a road with a particular direction, and each step it adds another tile of road next to the previous one. 90% of the time the next road tile will be placed by continuing in the current direction, 5% of the time it could turn left, and 5% of the time it could turn right.
If you want to play with Markov chains, learn more about them, and see them in action, then see Victor Powell’s visual explanation of Markov chains.